1tanx*tan2x = sec 2x LS =1 (sin x/cos x)(sin 2x/ cos 2x) =1 (sin x/cos x)(2sin x* cos x)/ cos 2x) =12sin^2(x)/(cos 2x) ={cos(2x) 2sin^2(x)}/cos (2x)Separate fractions Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by sin(x) cos(x) sin ( x) cos ( x) Convert from cos(x) sin(x) cos ( x) sin ( x) to cot(x) cot ( x) Divide sec2(x) sec 2 ( x) by 1 1 Rewrite sec(x) sec (Get an answer for 'Prove that tan^2x/(1tan^2x) = sin^2x' and find homework help for other Math questions at eNotes
2
5.25064634
5.25064634-The most general solutions of the equation sec^2x = root2(1 tan^2x) are given bySolution for tan (2x)sec (2x)dx 3 Physics Social Science
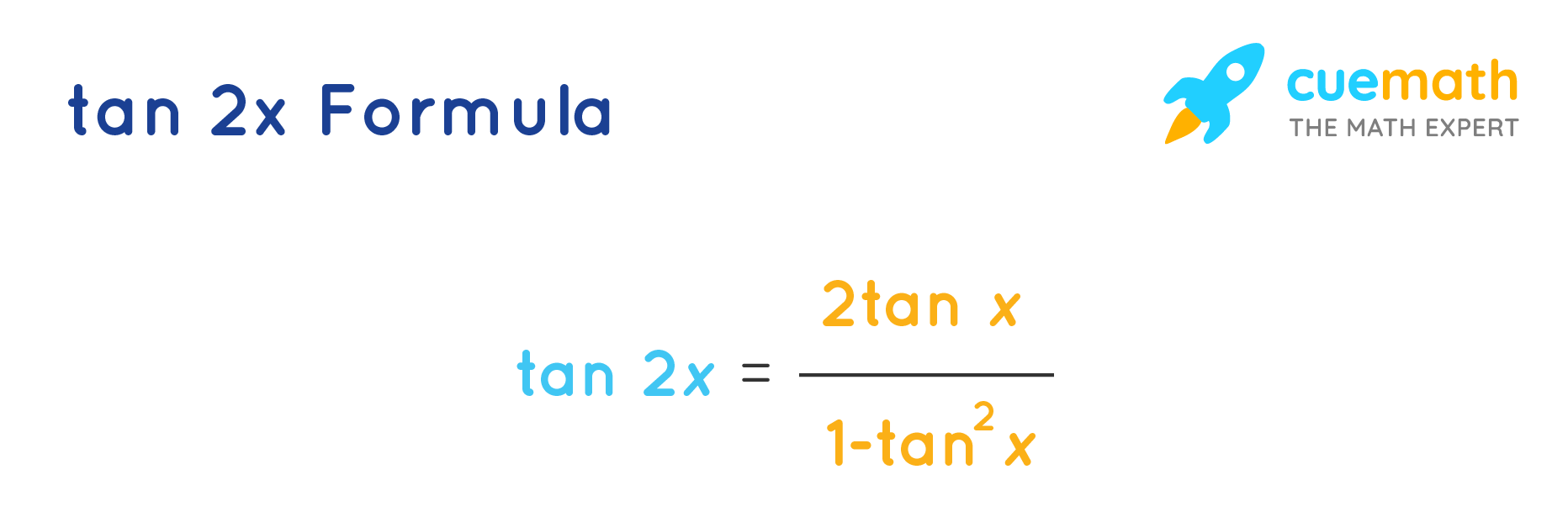



Tan 2x Formula What Is Tan 2x Formula Examples
Ex 34, 8 Find the general solution of the equation sec2 2x = 1 – tan 2x sec2 2x = 1 – tan 2x 1 tan2 2x = 1 – tan2x tan2 2x tan2x = 1 – 1 tan2 2x tan2x = 0 tan 2x (tan2x 1) = 0 Hence We know that sec2 x = 1 tan2 x So, sec2 2x = 1 tan2 2x tan 2x = 0 ta 证明过程如下:tan²x=sin²x/cos²x=(1cos²x)/cos²x=1/cos²x1=sec²x1。 运用证明的公式如下: (1)平方关系: sin^2(α)cos^2(α)=1 tan^2(α)1=sec^2(α) cot^2(α)1=csc^2(α) (2)积的关系: sinα=tanα*cosα cosα=cotα*sinα tanα=sinα*secα cotα=cosα*cscα secα=tanα*cscα cscα=secα*cotα (3)倒数关系: 采纳率: 100% 帮助的人: 164万 我也去答题 访问个人页 关注 展开全部 楼主,原式1tan^2x可化为: 已赞过 已踩过 < 你对这个回答的评价是?
Find the general solution of the equation sec^2 2x = 1 tan 2x LH S = tan2x secx 1 1 = sec2x −1 secx 1 1 = (secx 1)(secx − 1) secx 1 1 *You can now get rid of (secx1) at the top and bottom of the fraction When the numerator and denominator of a fraction are both the same, providing they aren't both zeros, what you get is 1 = secx − 1 1 = secx = RH SClick here👆to get an answer to your question ️ If tan^2xsecxa=0 has atleast one solution
If 2x = sec A and 2/x = tan A prove that (x^2 1/x^2 ) = 1/4 Sarthaks eConnect Largest Online Education Community If 2x = sec A and 2/x = tan A prove that (x2 1/x2) = 1/4 Login =(1cos²x)/cos²x =1/cos²x1 =sec²x1 因为secx=1/cosx 扩展资料 cotx乘tan2x=sec2x tan2x=2tanx/(1tanx的平方) 设tanx=t,则原方程变为: 2t/(1t^2)1/t=0 即:2t^2(1t^2)=0 t =±根号3/3 tanx =±根号3/3 可得x=kπ±π/6 x∈0,2π 所以x=π/6,5π/6,7π/6,11π/61年前 1个回答 求几个特殊三角函数值0 30 45 60 90的sin cos tan cot sec csc1楼的正割和余割?




Pstrigonometric Equations Trigonometric Functions Equations




1 Sin 2x Tan 2x Sec Sec 2 X Csc 2x 1 1 C Gauthmath
The values of x and y which satisfy the equation 1 2 sin x 5 cos x = 2 y 2 − 8 y 2 1 are View solution If tan A is an integral solution of the inequality 4 x 2 − 1 6 x 1 5 < 0 and cos B is equal to slope of the bisector of the angle in the first quadrant between the x and y axes, then the value of sin ( A − B ) sin ( A B ) isTan^2xsec^2x/1tan^6x Ask questions, doubts, problems and we will help youA)cot x b)csc x c)tan x d)sec x tan x Please help me ( Math What is a simplified form of the expression sec^2x1/(sinx)(secx)?




Cos 2x




Consider The Following Equations 1 Cosec 2x Sec 2x Cosec 2xsec 2x 2 Sec 2x Tan 2x Sec 2xtan 2x 3 Cosec 2x Tan 2x Cot 2x
What is a simplified form of the expression sec^2x1/sin x sec x ? answered by Ria (548k points) selected by faiz Best answer sec θ tan θ = 1/4x 1/4x = 1/2x Please log in or register to add a commentFound 2 solutions by ewatrrr, MathLover1 Answer by ewatrrr () ( Show Source ) You can put this solution on YOUR website!



Chapter 5
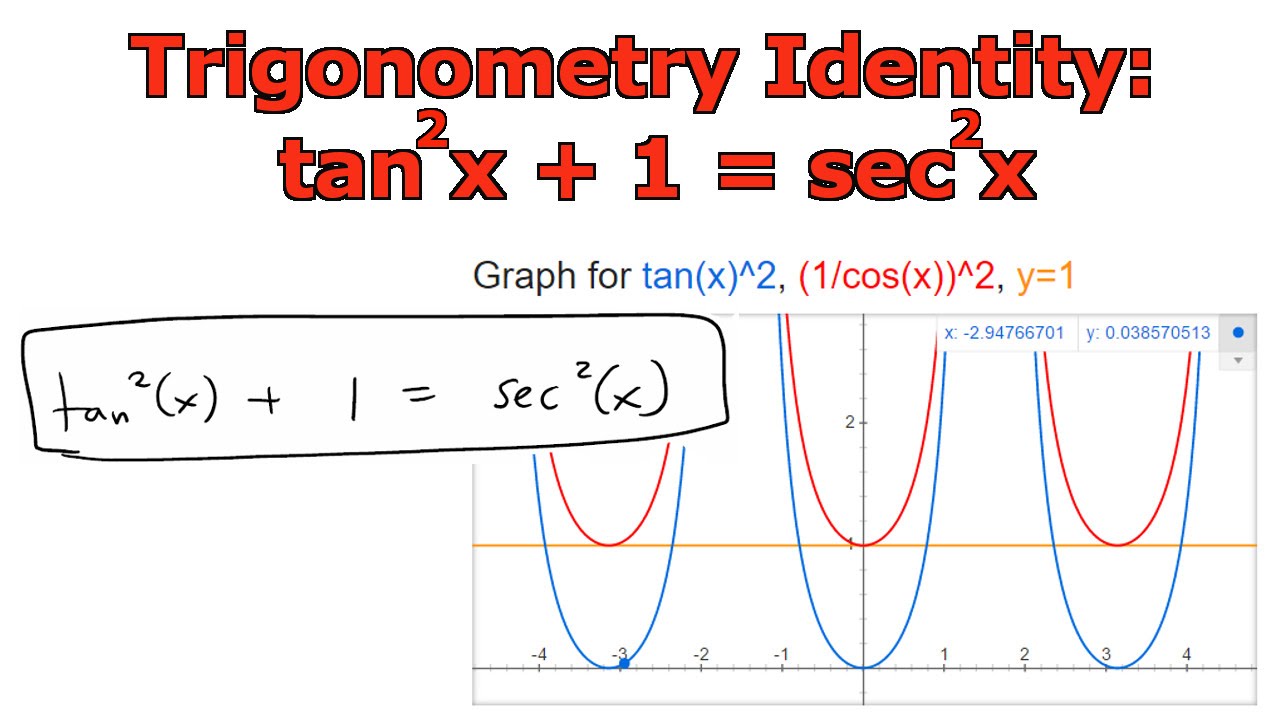



Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube
Tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx Integral of the function \frac {\cos ^2 x} {1\tan x}Differentiate wrt x \frac {2\tan (2x1)} {\cos (2x1)} cos(2x−1)2 tan(2x−1) View solution steps Steps Using Chain Rule \sec ( 2x1 ) sec ( 2 x − 1) If F is the composition of two differentiable functions f\left (u\right) and u=g\left (x\right), that is, if F\left (x\right)=f\left (g\left (x\right)\right), then the derivative of F is theTan^2xtan^2y=sec^2xsec^2y and, how do you factor and simplify, cscx(sin^2xcos^2xtanx)/sinxcosx Inverse trigonometry Prove that tan^1(1/2tan 2A)tan^1(cotA)tan^1(cot^3A) ={0,ifpi/4 math (trigonometry) A=170 degree then prove that Tan A/2=1rot(1Tan^2 A)/Tan A math
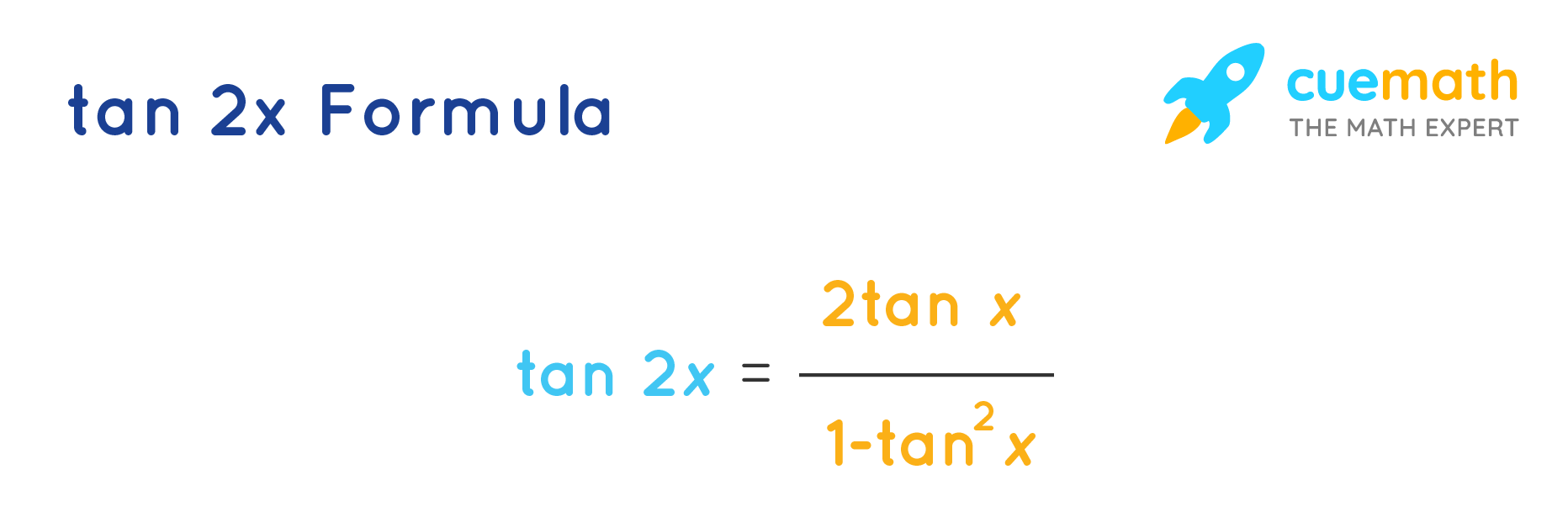



Tan 2x Formula What Is Tan 2x Formula Examples
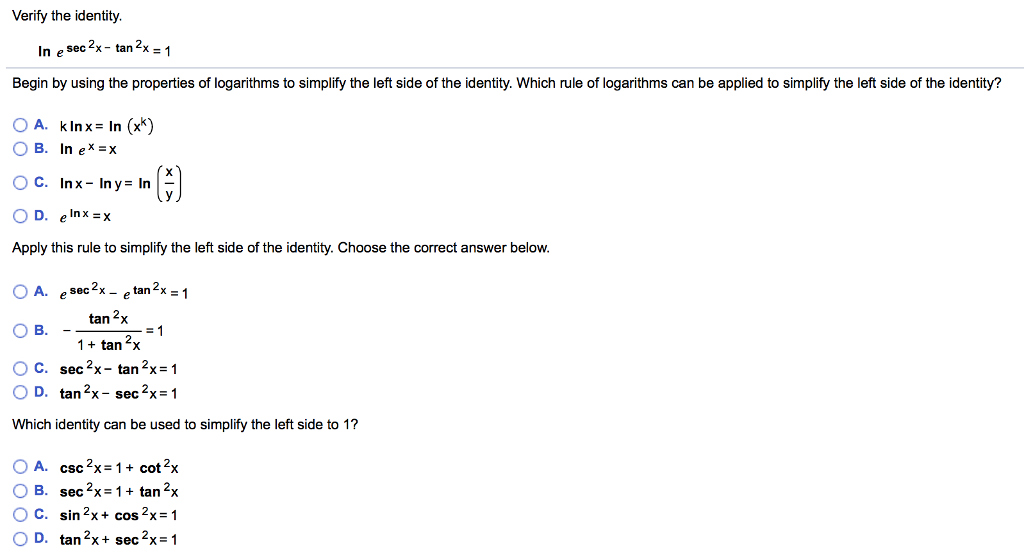



Verify The Identity In Esec 2x Tan 2x 1 Begin By Chegg Com
$$\sec^2 x \tan^2 x = 1$$ I notice that $\tan^2 x 1 = \sec^2 x$ so I tried substituting $\sec^2 x$ with $\tan^2 x 1$ I get $$\tan^2 x 1 \tan^2 x = 1 \tag{1}$$ Then I try to solve by using the zero product property, so I subtract 1 from the right side of the equation Leaving me with $$\tan^2 x \tan^2 x = 0 \tag{2}$$ (sec(x) sen²(x) cos²(x)) (sec(x) 1) = tan²(x)Existe una identidad que dicesen²(x) cos²(x) = 1Entonces(sec(x) 1)(sec(x) 1) = tan²(x)sec²(x) 1 = ta the number of solution of the equation tan^2xsec^(10)x1=0 in (0,10) is Updated On 187 To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now!
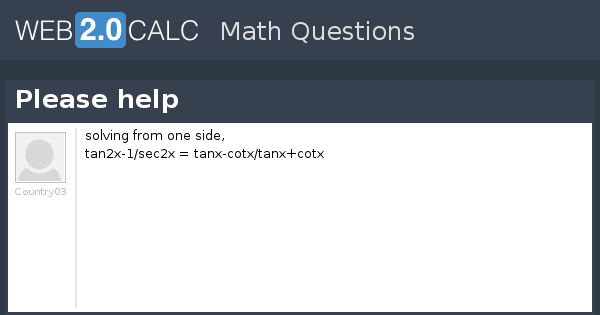



View Question Please Help



Prove The Identity Tan P 4 X Tan P 4 X 2 Sec 2x Sarthaks Econnect Largest Online Education Community
`int tanx sec^2x sqrt(1tan^2x) dx` `int tanx sec^2x sqrt(1tan^2x) dx` Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P Bahadur IITJEE Previous Year Narendra Awasthi MS Chauhan Biology NCERT NCERT Explanation This is readily derived directly from the definition of the basic trigonometric functions sin and cos and Pythagoras's Theorem Confirming that the result is an identity Yes, sec2 − 1 = tan2x is an identityCalculus Solve for x tan (2x)=1 tan (2x) = 1 tan ( 2 x) = 1 Take the inverse tangent of both sides of the equation to extract x x from inside the tangent 2x = arctan(1) 2 x = arctan ( 1) The exact value of arctan(1) arctan ( 1) is π 4 π 4 2x = π 4 2 x = π 4 Divide each term by 2 2 and simplify




3 Sec 2x1 Cos2 X Tan 2x Tantx E Sus S Always The An 0 Om Reddit Meme On Me Me




How Do You Prove Tan 2x Secx 1 1 Secx Socratic
Get answer sec ^(2) 2x =1tan 2x Apne doubts clear karein ab Whatsapp par bhi Try it nowYes, sec 2 x−1=tan 2 x is an identity sec 2 −1=tan 2 x Let us derive the equation We know the identity sin 2 (x)cos 2 (x)=1 ——(i) Dividing throughout the equation by cos 2 (x) We get sin 2 (x)/cos 2 (x) cos 2 (x)/cos 2 (x) = 1/cos 2 (x) We know that sin 2 (x)/cos 2 (x)= tan 2 (x), and cos 2 (x)/cos 2 (x) = 1 So the equation (i) after substituting becomes tan 2 (x) 1= 1Watch Video in App



2



What Is Math Int Tan 2 2x Dx Math Quora
Respuesta Explicación paso a paso (1tan^2x)cosx=secx , cuales identidades son 1tan^2x=sec^2x cosx = 1/secx (1tan^2x)cosx=secx sec^2x (1/secx)=secx sec^2xHi Simplifying the following (sec^2x csc^2x) (tan^2x cot^2x) tan^2x = sec^2x 1 cot^2x = csc^2x 1 (sec^2x csc^2x) (sec^2x 1 csc^2x 1)= 2👍 Correct answer to the question Prove that tan^2x sec^2x=1 eeduanswerscom




Omtex Classes Iv Sec6x Tan6x 1 3 Sec2x Tan2x
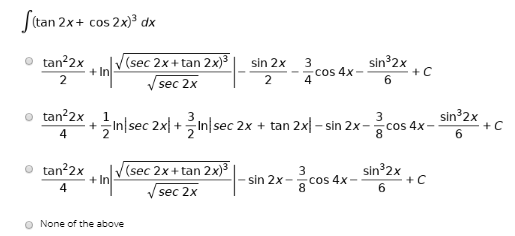



Answered Stan 2x Cos 2x Dx Tan 2x 2 V Sec 2x Bartleby
A cot x b csc x c tan x***** d sec x tan x I think this is the correct answer, but I do not understand why Can someone please explain?To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `sec^(2)2x=1tan2x`Integration of sec^2x/1tan x (Solution)Integration of sec^2x/1tan x (Solution) dx this video teaches us how to Integration of sec^2x/1tan x (Solution) d



Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero



1
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreRewrite sec(x) sec ( x) in terms of sines and cosines Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by 1 cos(x) 1 cos ( x) Write cos(x) cos ( x) as a fraction with denominator 1 1 Cancel the common factor of cos(x) cos ( x)Lista över trigonometriska identiteter är en lista av ekvationer som involverar trigonometriska funktioner och som är sanna för varje enskilt värde av de förekommande variablerna De skiljer sig från triangelidentiteter, vilka är identiteter som potentiellt involverar vinklar, men även omfattar sidolängder eller andra längder i en triangel




Bhasvic Maths 1 A1 Doubles Assignment 12a Ppt Download




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
Identity\\sin(2x) identity\\cos(2x) identity\\sin^2(x)\cos^2(x) trigonometricidentitycalculator Prove sec^{2}xtan^{2}x=1 en Related Symbolab blog posts I know what you did last summerTrigonometric Proofs To prove a trigonometric identity you have to show that one side of the equation can be transformed into the other HOPE IT HELPS Vote helpful if it does !!!! If tan x = t then tan 2x sec 2x is equal to A \(\frac{1 t}{1 t}\) B \(\frac{1 t}{1 t}\) C \(\frac{2t}{1 t}\) D \(\frac{2t}{1 t}\)




Is There Any Other Way To Establish This Trig Identity Frac Sec X 1 Tan X Frac Sin X 1 Cos X Mathematics Stack Exchange




Trig Identities The Student Room
Find an answer to your question tan^2x 1 = sec^2x PROVE hopelafave is waiting for your help Add your answer and earn pointsVerify $$\sec^2x \tan^2x = (1\sin^4x)\sec^4x$$ My solution $$ \begin{align}\sec^2x\tan^2x&=\frac{1}{\cos^2x}\frac{\sin^2x}{\cos^2x}\\ &=\frac{1\sin^2x}{\cos(1\times2) (1\times3) (1\times4) (1\times5) (1\times6) (2\times1) (3\times1) (4\times1) (5\times1) (6\times1) (7\times1)
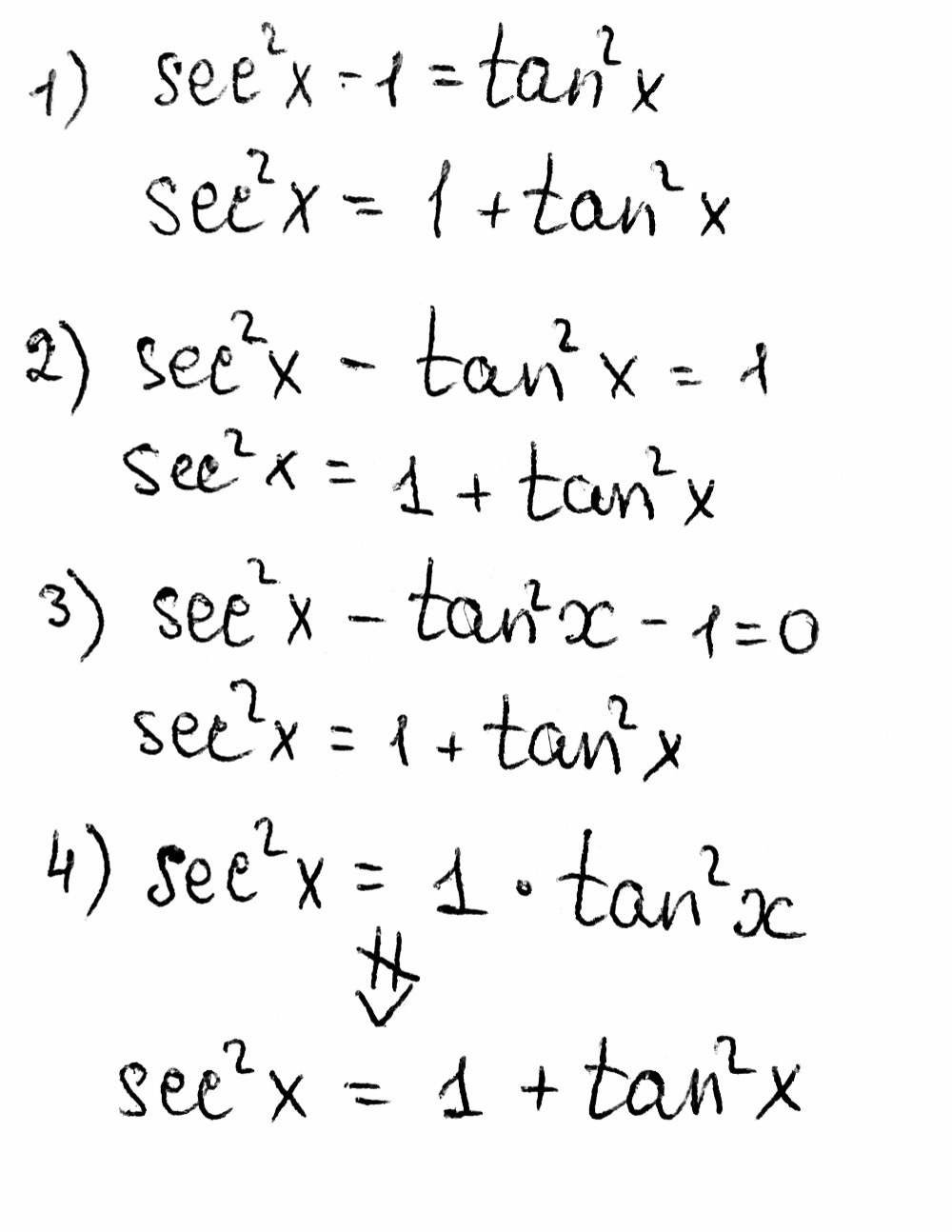



Which One Is Not Equivalent To Sec2x 1 Tan2x Sec Gauthmath
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction
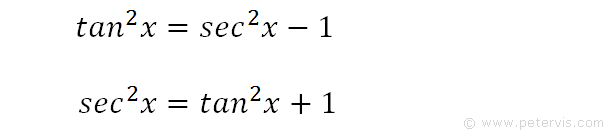



Integrate Sec 2x Method 1




Answered Tan 2x Sec N 2x Sec 2x Dx Bartleby




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic




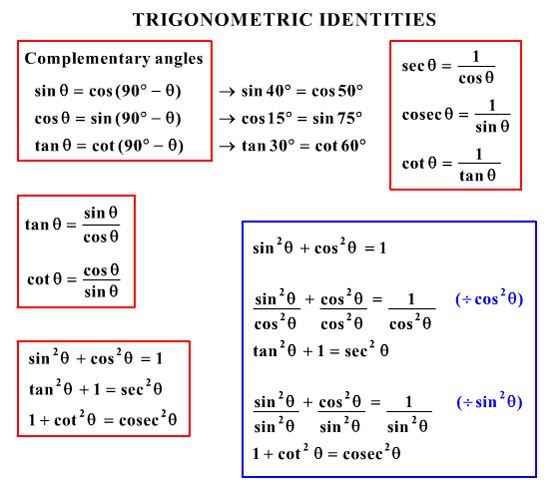
Math34 Trigonometric Formulas
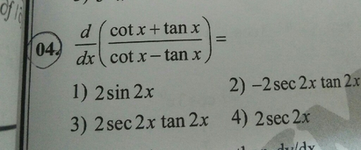



D Cotx Tanx Dx Cot X Tan X 1 2sin 2x 04 2 2 Sec 2x Tan 2 Scholr
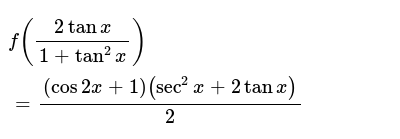



F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2




Frac Tan 2x 1 Sec 2x Tan X Snapsolve



Tan 2x Sec 2x 1 Also Tan Sec 1 Or Am I Missing Something Physics Forums



Tan2x ただの悪魔の画像




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic
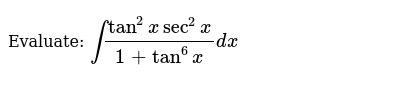



Evaluate Int Tan 2xsec 2x 1 Tan 6x Dx




I M Seriously Confused About This Trigonometry Problem Askmath




Solve 4tan 2x 2sec 2x 1 0 X Belongs To 0 Maths Trigonometric Functions Meritnation Com



1



How To Integrate X Sec 2x Tanx Dx Quora




Ppt Analytic Trig Powerpoint Presentation Free Download Id



Integration Of Sec 2x 1 Tan 2x Maths




Differential Equation D 2 1 Y E X Sec 2 X Tan X Mathematics Stack Exchange
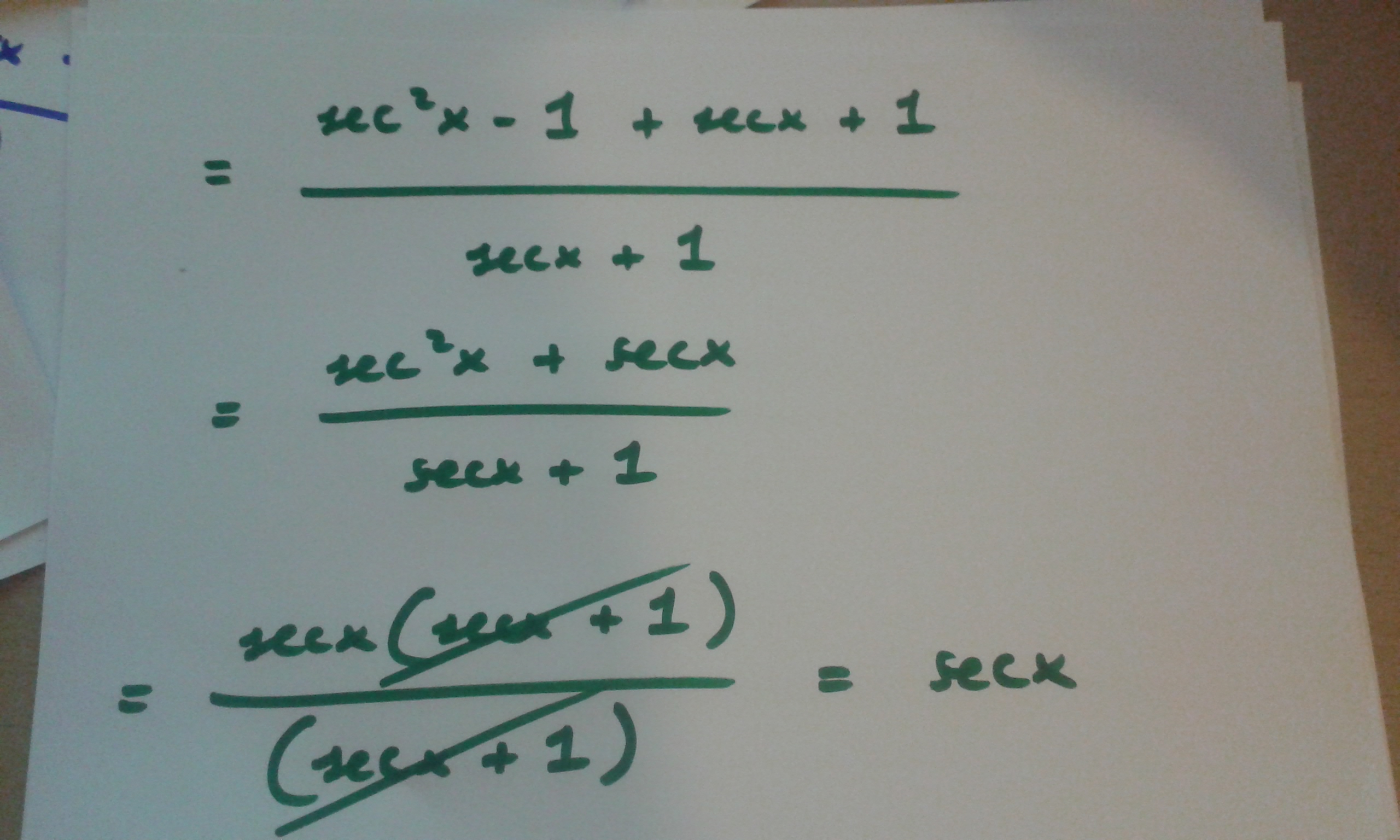



How Do You Prove Tan 2x Secx 1 1 Secx Socratic



1



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero



2




Tan2x ただの悪魔の画像




How To Show That Math Tan 2 X Sec 2 X 1 Math Quora




How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Homeworklib




Tan 2x Sec 2x 1 True Or False For All Values Of X Wyzant Ask An Expert




Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified



2 Secx 1 Secx 1 Br Answer




If Y Tan 2x Sec 2x Find Dy Dx Brainly In
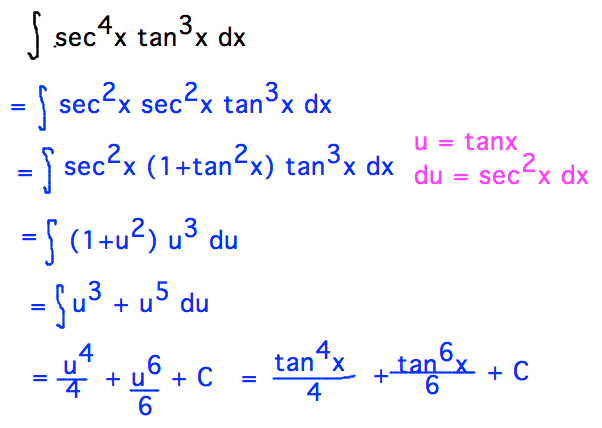



Geneseo Math 222 01 Trigonometric Integration




Limit Trigonometric Function 2 Sec 2x 1 Tan X Youtube



2




Mapping Your Mind By Kyanna Dyer
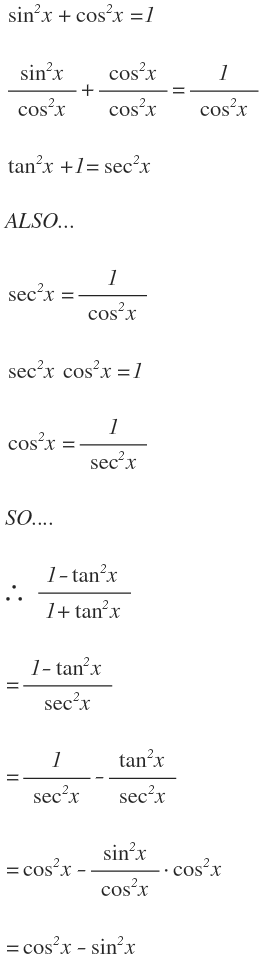



How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic




Get Answer 1 Tan2x Sec2x Dx Sin2x 2 C Tan 2 X 2 C 2sin X Cos X Transtutors
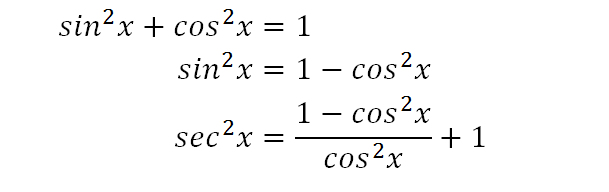



Integrate Sec 2x Method 2




Int Tan 2x Secx 1 Dx Youtube



What Would Be Steps In Proving That Tan2x Secx 1 1 Sec X Socratic
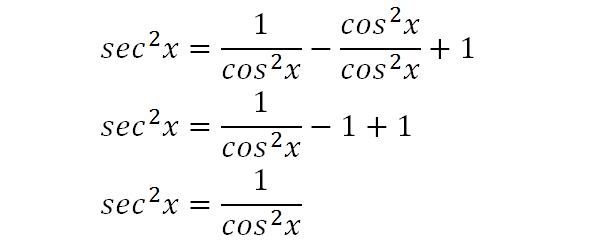



Integrate Sec 2x Method 2
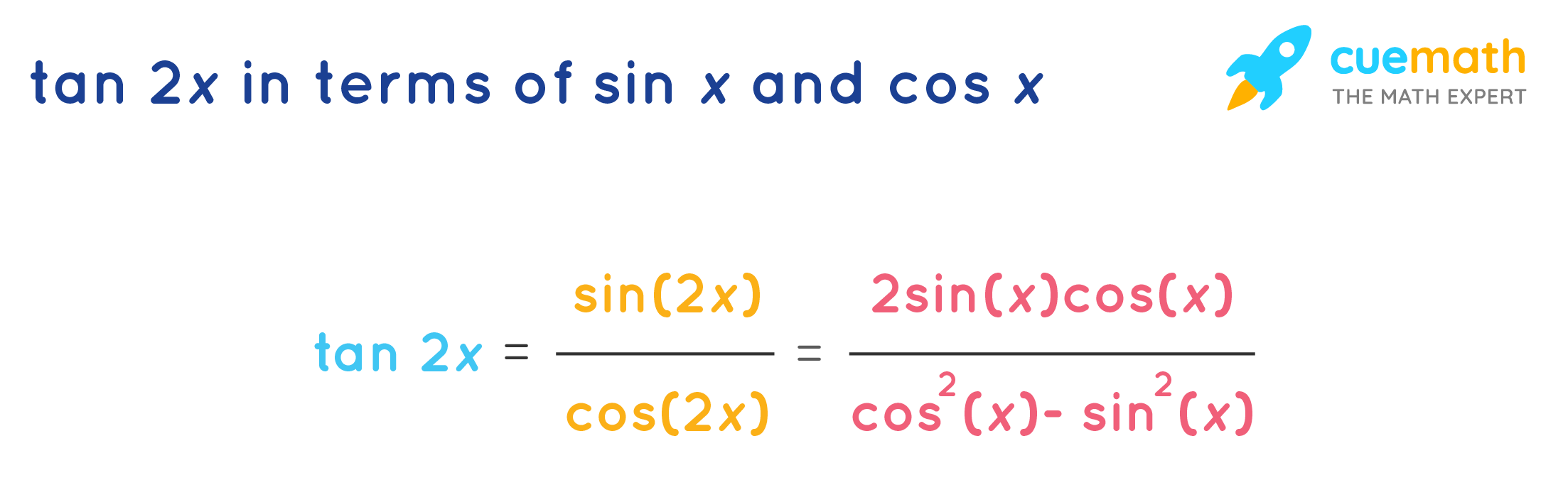



Tan 2x Formula What Is Tan 2x Formula Examples




Solve Tan 2 X 1 0 Yahoo Answers Noha Matthieu Lire Un Livre



How Do We Prove That Tan2x 1 Sec2x Tanx Quora




Ex 7 3 15 Integrate Tan3 2x Sec 2x Class 12 Ncert Ex 7 3




1 Tan1 1 Tan2 1 Tan3 1 Tan45 2 N Brainly In Ryad Antonio Ebooks En Ligne Gratuit




Sec 1 1 Tan 2x 1 Tan 2 X
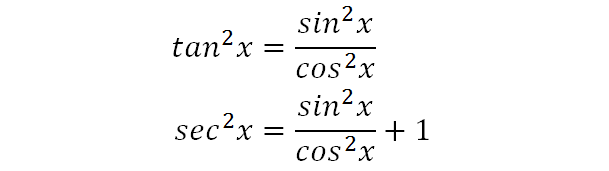



Integrate Sec 2x Method 2
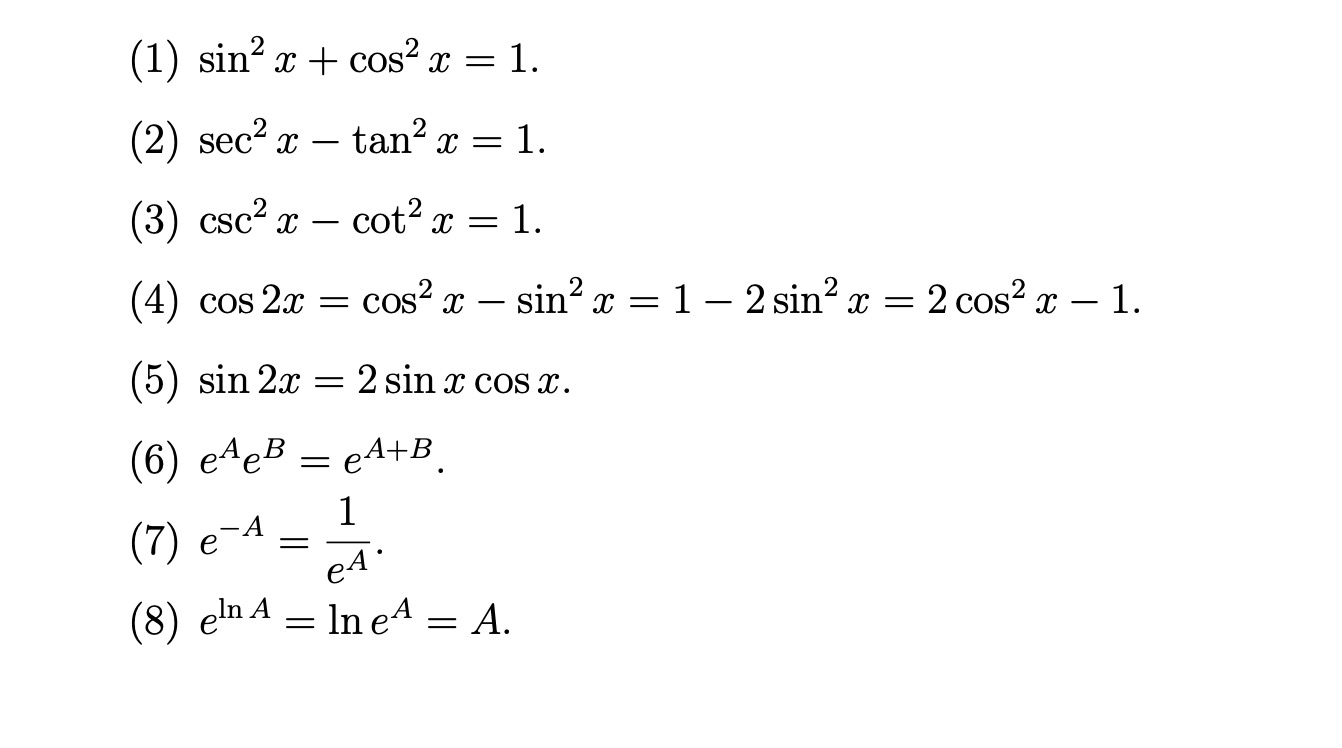



Here Is A List Of Identities Involving Trigonometric Chegg Com



Integral 1 Tan 2 X Sec 2 X Youtube



2




2 Prove The Following Trig Identities A Prove Tan Chegg Com
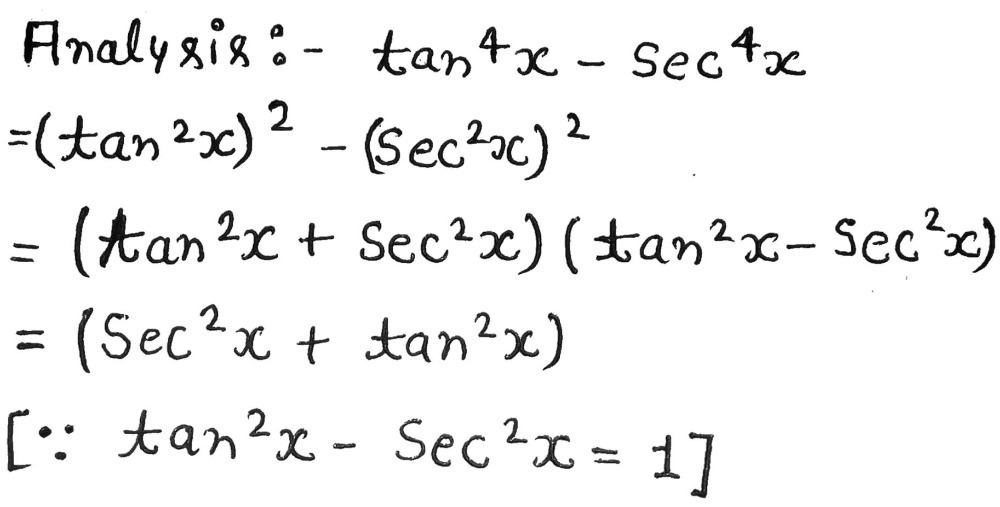



Complete The Identity Tan 4x Sec 4x Sec 2x Tan 2 Gauthmath




Analytic Trig Trig Identities Sin 2x Cos 2x 1 Tan 2x 1 Sec 2x 1 Cot 2x Csc 2x Sin X Sinx Cos X Cosx Tan X Tanx Ppt Powerpoint




Trig Identity Sec2x Minus Tan2x T10 Youtube




Differentiate The Following From First Principle Tan 2x 1




3 Sec 2x1 Cos 2x Tan 2x Tan X Esus Is Always The Anse Ja Irl Meme On Me Me



Proof Tan 2 1 Sec 2 Youtube




Find All Solutions To Tan 2x Secx 1 Wyzant Ask An Expert




3 Sec 2x1 Cos2 X Tan 2x Tan X Jesus S Always The An イ Es No U One Of My Favorite Posts This Is Ridiculously Hilarious Houstonsfavoriteatheist Godtheskeptic I Might Try This




Solution Calculations Studypool
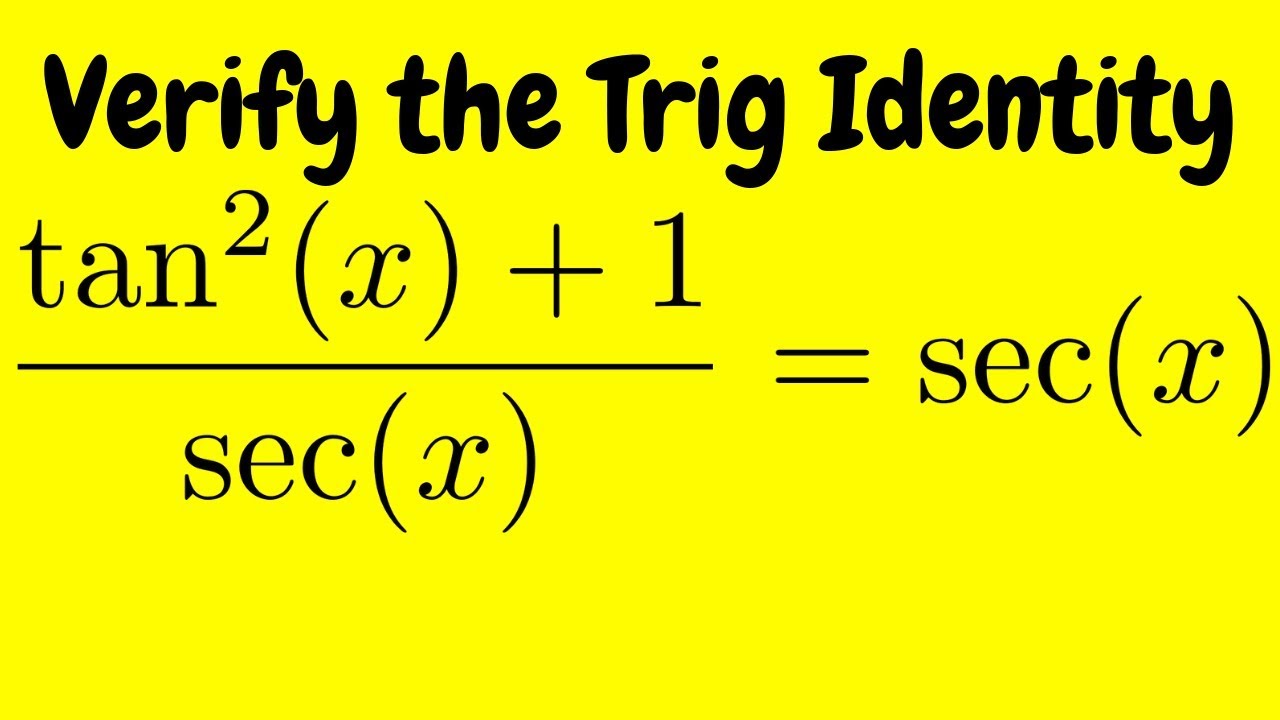



Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube
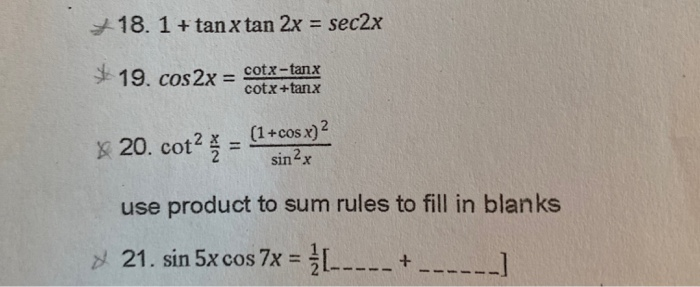



18 1 Tan X Tan 2x Sec2x 19 Cos2x Cotx Tank Chegg Com



2




Mathematics Question Of The Day With Solution Facebook



2



2



3




Tan X Sec 2x 1 Make The Left Hand Side Match The Right Side Brainly Com
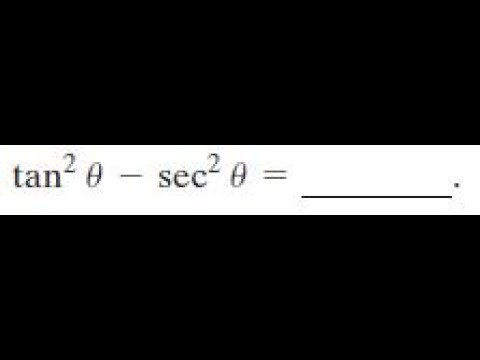



Tan 2x Sec 2x Youtube




Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com
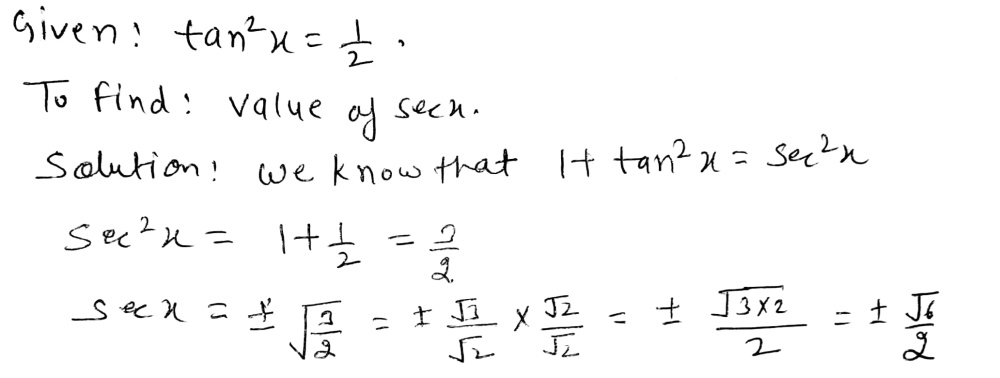



46 Find Sec X If Tan 2x 1 2 A 1 4 B Gauthmath




3 Sec 2x1 Cos2 X Tan 2x Tantx E Sus S Always The An 0 Om Sec Meme On Me Me




The Derivative Of Sec2x Derivativeit




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
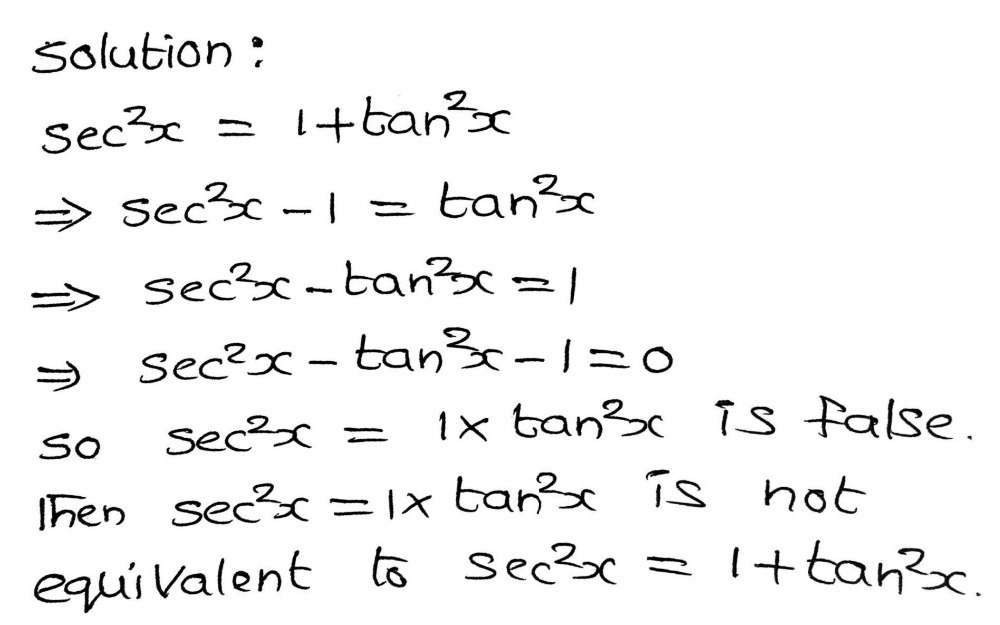



Which One Is Not Equivalent To Sec2x 1 Tan2x Sec Gauthmath




Answered 3 1 Tanx Tan 2x Sec 2x S Bartleby



Tan2x Sec2x ただの悪魔の画像




3 Sin Differentiate The Following Functions With Respect Tox 1 Sin 2x 4 Sin 1 Ax




How Do You Integrate 1 Tan2x Sec2x Dx Socratic



0 件のコメント:
コメントを投稿